Advanced Usage
Additional inputs to solving routines
Specifiying the Number of Variables Explicitly
num_variables is an optional parameter to
eqc_direct.client.EqcClient.solve_integer() and eqc_direct.client.EqcClient.solve_integer(), which defaults to the number of
variables inferred from the poly_indices argument, i.e., the largest integer
appearing over all the indices. However, a user may specify additional variables that do
not appear explicitly in poly_indices. Typically, this is only one additional
variable, which creates slack with respect to the sum_constraint, and whose value
does not affect the value of the objective function.
As a simple example, if num_variables=3 and sum_constraint=1 so that
with the objective function given as
then , , and is a viable solution (giving
the ground-state energy ). However, if were omitted by using
the default num_variables=2, then and would not be a
viable solution because it would violate the corresponding sum constraint
Lastly, due to domain restriction , can only take up so much slack in the problem, so that the subdomain for and is enlarged but still limited.
Specifiying More than One Sample
The Dirac-3 device is a stochastic solver, and furthermore some problems have multiple solutions that give the same minimum energy. Both of these considerations may indicate the need to run multiple samples that solve the same problem repeatedly on the device. num_samples is an optional parameter to both eqc_direct.client.EqcClient.solve_integer() and eqc_direct.client.EqcClient.solve_integer(), which defaults to one sample. Pass an integer greater than one to run multiple samples more efficiently as a “batch” in a single job. Additionally, running multiple samples in a single batch can save some time in pre-processing since it is only necessary to apply the formatting to submit the problem to the device a single time.
Device Configurations
Dirac-3 allows users to control the optimization process using the relaxation schedule parameter. This parameter controls the time allocated for the system to evolve and converge towards the ground state and is available for both solver types.
Schedules 1, 2, 3, and 4 correspond to different time settings, with higher schedule numbers indicating slower system evolution. Consequently, this leads to a higher probability of obtaining favorable results. Additionally, there are two different device settings that can modify each relaxation schedule:
- mean_photon_number: Sets the average number of photons present in a given quantum state. Allowed range: [0.0000667, 0.0066666].
quantum_fluctuation_coefficient: specifies the number of photons () for each feedback loop which controls the shot noise. The number of photons is inversely related (e.g. increasing number of photons decreases noise; fewer photons increases noise) to the shot noise with the following equation:
Allows integer values from [0,100].
If not specified, the system defaults for each schedule will be applied. These parameters are still an active area of research, so manipulation from standard schedules is considered experimental. Below is an example of a parameter sweep taken for LABS 10:
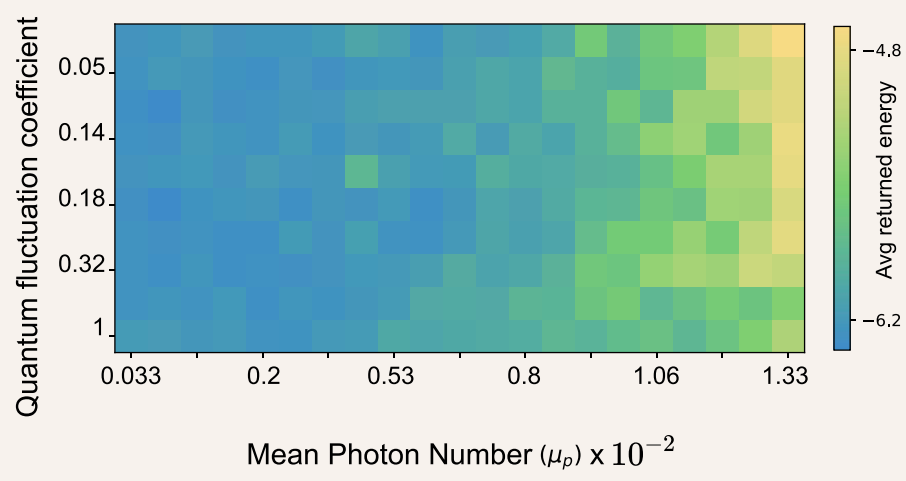
A sweep of values for mean_photon_number and quantum fluctuation coefficient on problem QPLIB0018 from the library of quadratic programming instances (QPLIB) (Furini et al, 2018)
An example using relaxation schedule with tuned parameters
Find the minimium of:
where and are both in , i.e, minimizing over a non-integral lattice in the positive quadrant.
By inspection, we can see that, without any domain restriction, has a unique global minimum of zero at and . However, that solution is not on the lattice domain, so one expects the optimal feasible solution to be and with .
We now verify this using using Dirac-3. First, expand as a polynomial:
Dropping the constant terms, which do not affect the minimization problem and are not supported by Dirac-3, gives:
This minimization problem does not appear to be particularly hard, so we will start with
relaxation_schedule=1. We need to choose a sum_constraint, num_variables,
and solution_precision to search a sufficiently large portion of the domain lattice
spaced at 0.5 in each variable. This can be difficult in larger dimensional problems
where one has less insight as to where the optimal solution may lie. Furthermore, the
sum constraint means that the domain searched forms a non-rectangular
simplex. To this end, we take
num_variables=3, sum_constraint=3, and solution_precision=0.5, so that the
constrained domain is large enough to encompass the region where we suspect the optimal
solution to lie. Lastly, we set num_samples=5 to examine repeatability.
- from pprint import pprint
- import numpy np
- from eqc_direct.client import EqcClient
- # MUST FILL IN THE VALUES IN THIS FROM YOUR NETWORKING SETUP FOR THE DEVICE
- client = EqcClient(ip_address="<YOUR DEVICE IP ADDRESS>", port="<YOUR DEVICE PORT>")
- poly_indices = np.array([[0, 1], [0, 2], [1, 1], [2, 2]], dtype=np.uint32)
- poly_coefficients = np.array([-2.0, -2.75, 1.0, 1.0], dtype=np.float32)
- # use lock to prevent other users from taking exclusive access to the device
- lock_id, start_ts, end_ts = client.wait_for_lock()
- print(f"Waited for lock: {(end_ts - start_ts) / 1e9} s for lock_id={lock_id}.")
- try:
- result = client.solve_sum_constrained(
- lock_id=lock_id,
- poly_indices=poly_indices,
- poly_coefficients=poly_coefficients,
- num_variables=3,
- sum_constraint=3,
- solution_precision=0.5,
- mean_photon_number=0.00333,
- quantum_fluctuation_coefficient=4,
- num_samples=5,
- )
- print("Total execution time (s):",
- np.array(result["preprocessing_time"])+np.array(result["postprocessing_time"])+np.array(result["runtime"]))
- pprint(result)
- finally:
- # release lock when finished using the device
- lock_release_out = client.release_lock(lock_id=lock_id)
- print(f"Lock release returned {lock_release_out}")
Additional Resources
To learn more about the theory and function of the device please use the followign resources:
Troubleshooting and Support
If you encounter any issues or errors that are not covered in this manual or the user guide for the device and require additional assistance contact our customer support at https://quantumcomputinginc.ladesk.com.